Brücken-Challenge
- Lies und verstehe die Aufgabe
- Sieh dir das Video von Lauri und Anni Vuohensilta aus Finnland an:
- Nimm an der Challenge teil
- Bedingungen der Challenge
- Abmessungen für deine Brücke
- Material
- Entwirf deine eigene Brücke
- Konstruiere deine Brücke
- Schicke deine Brücke als
.stlDatei an Herrn Frühling - 3D-Druck der Brücke
- Wie viel hält deine Brücke aus?
- Wie funktioniert der „Brücken-Knacker“?
- Wie die Kraft gemessen wird
- Welches Gewicht hat die Brücke im Beispiel ausgehalten?
- Welches Gewicht hält deine Brücke aus?
- Ein Video vom Belastungstest deiner Brücke …
Lies dir die Aufgabenstellung genau durch und frag Herrn Frühling, wenn dir etwas nicht klar ist. Schreibe eine E-Mail an: jan [dot] fruehling[at]mbs [dot] hamburg [dot] de(Eine Frage zur 3D-Druck Brücken-Challenge)
Die beiden veröffentlichen auf YouTube Videoclips, in denen sie Sachen mit einer hydraulischen Presse kaputt machen.
In dem Video siehst du verschiedene Modelle von Brücken. Welche sind stabil, welche nicht so? Wie könnte deine Brücke aussehen?
Schreibe eine E-Mail an Herrn Frühling, dass du teilnehmen möchtest. Du bekommst dann einen Namen und ein Passwort für die Teilnahme. Schreibe eine E-Mail an: jan [dot] fruehling[at]mbs [dot] hamburg [dot] de(3D-Druck Brücken-Challenge). Gerne kannst du als Gruppe teilnehmen.
Deine Brücke darf sich bei Belastung nicht mehr als $ 4mm $ durchbiegen.
Deine Brücke soll möglichst leicht sein. Wenn du das Programm Prusa Slicer heruntergeladen hast (das Programm wird weiter unten erklärt), kannst du die Masse des 3D-Drucks ermitteln. Weniger als $ 0,02 kg $ ist eine gute Masse (das sind 20 Gramm).
Deine Brücke soll mit mindestens $ 150 kg $ belastbar sein. Wie der Belastungstest funktioniert, liest du weiter unten.
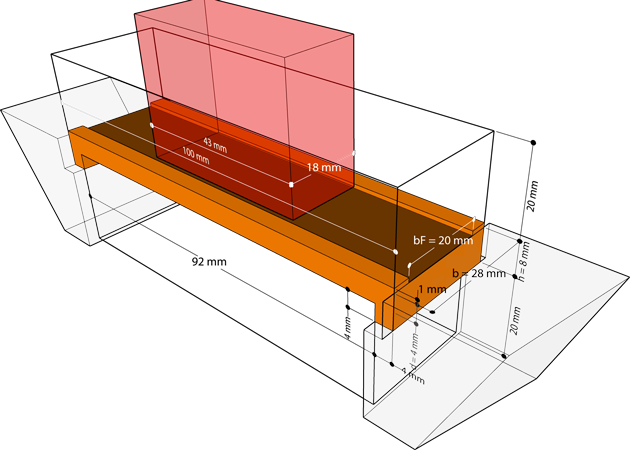
Klicke auf das Bild, um es zu vergrößern.
| Länge | l = | 100 mm |
| Breite | b = | 28 mm |
| Breite der Fahrbahn | bF = | 20 mm |
| Dicke der Fahrbahn | d = | 4 mm |
| Abstand zwischen den Widerlagern der Brücke | a = | 92 mm |
| Auflagefläche der Widerlager | AWl = | 4 mm × 28 mm |
| Höhe des Auflagers der Brücke am Widerlager | h = | 8 mm |
| 3D-Druck-Fülldichte in massiven Bauteilen | Infill = | 15 % |
Beim Belastungstest drückt ein „Stempel“ auf deine Brücke. Dieser Stempel ist im Bild oben rot eingefärbt und hat die Abmessungen 43 mm × 18 mm.
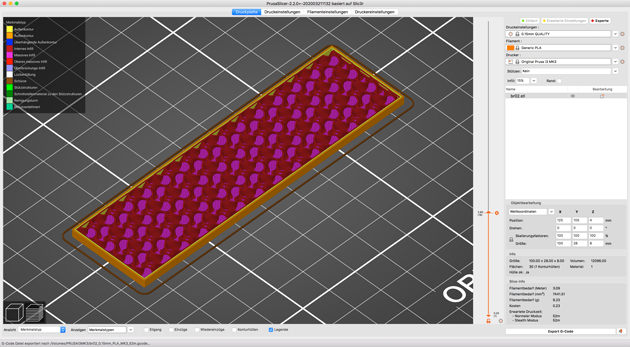
Auf diesem Bild siehst du die Füllung (Infill) in dickeren Bauteilen:
Deine Brücke wird in PLA (Polylactide) gedruckt. PLA ist ein biologisch abbaubarer Polyester, welcher recht gute mechanische Eigenschaften aufweist.
So sieht die einfachste Brücke aus, die den vorgegebenen Abmessungen entspricht:
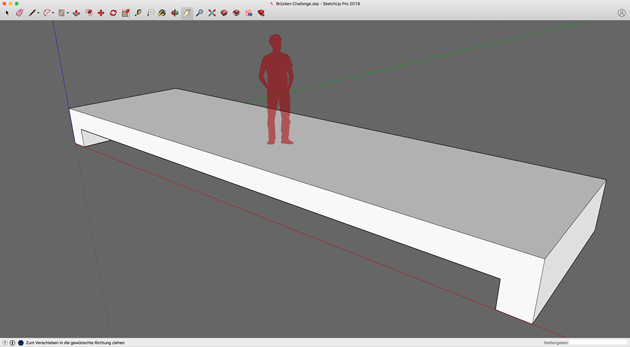
Diese Brücke wird sich unter Belastung allerdings stark durchbiegen.
Zum Konstruieren deiner Brücke benutze bitte die kostenlose Software TinkerCAD. TinkerCAD ist web-based, du brauchst kein Programm herunter zu laden und zu installieren. Das Programm läuft in deinem Browserfenster. Finde heraus, was du mit TinkerCAD alles machen kannst. Hier sind ein paar Videos.
TinkerCAD Klassencode für WP II Natur und Technik 10: TTEUI62E7V2U.
TinkerCAD Klassencode für die Werkstatt Makerspace: 7C22E6DKW1ZJ.
Benutze zur Anmeldung den Spitznamen, den du von Herrn Frühling bekommen hast.
Wenn du Fragen hast, kontaktieren Herrn Frühling gerne über iServ.
Exportiere deinen Entwurf als .stl Datei.
.stl steht für STereoLithographie und ist das Dateiformat aus dem der Prusa Slicer den G-Code für den 3D-Drucker generiert. Prusa Slicer ist das Programm, welches eine Datei erstellt, die der 3D-Drucker verarbeiten kann.
Das Programm Prusa Slicer ist kostenlos. Du kannst es gerne herunterladen, um zu sehen, wie viel Zeit und Material deine Brücke im Druck braucht.
Die E-Mail-Adresse findest du weiter oben, in der rechten Spalte dieser Seite.
Herr Frühling druckt dann deine Brücke auf dem 3D-Drucker der #MachBar! (die #MachBar! ist der Makerspace der MBS. Der 3D-Drucker der #MachBar! ist ein Prusa i3 MK3.

Wenn deine Brücke fertig gedruckt ist, wird sie in einen „Brücken-Knacker“ eingespannt und einem Belastungstest unterzogen.
ACHTUNG! Die Brücke darf sich beim Belastungstest nicht mehr als $ 4 mm $ durchbiegen.
Was du auf dem Bild siehst: Links ist der Drehpunkt des Hebels, der kurze Hebelarm ist dort wo die kleine orangene Brücke eingespannt ist, der lange Hebelarm dort, wo ganz rechts das violette Seil befestigt ist.

Im Bild unten siehst du eine einfache Brücke in den „Brücken-Knacker“ eingespannt. Links und rechts der Brücke befinden sich die beiden Widerlager, welche die senkrechten Kräfte aufnehmen, die auf die Brücke wirken. In der Mitte drückt der „Stempel“ auf das Brückenmodell.

In diesem Video siehst du, wie der „Brückenknacker“ eine kleine Brücke knackt.
Diese filigrane Brücke bringt eine Masse von $ 0,014 kg $ auf die Waage.
Der „Brücken-Knacker“ sieht aus, wie ein großer Nussknacker. Physikalisch ist der „Brücken-Knacker“ ein einseitiger Hebel – langer und kurzer Hebelarm $ { l }_{ 1 } $ und $ { l }_{ 2 } $ befinden sich auf der gleichen Seite vom Drehpunkt $ DP $.
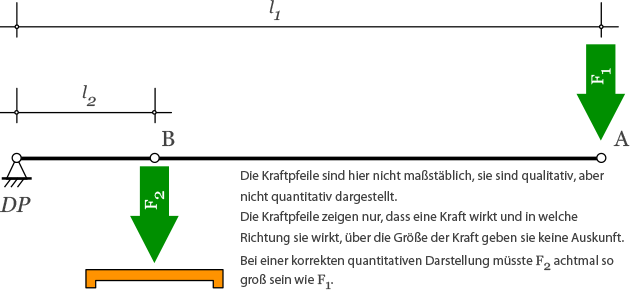
Wird auf den Hebelarm am Punkt $ A $ eine Kraft $ { F }_{ 1 } $ ausgeübt, so können wir mit dem Hebelgesetz ausrechnen, wie groß die Kraft $ { F }_{ 2 } $ ist, die am Punkt $ B $ in diesem Fall auf die Brücke wirkt. Hier drunter steht, wie das geht.
$ F $ ist das Formelzeichen für Kraft und Newton, abgekürzt $ N $, ist die Einheit für Kraft.
Hebelgesetz
$ { F }_{ 1 } \times { l }_{ 1 } = { F }_{ 2 } \times { l }_{ 2 } $
Praktische Anwendung
Gegeben sind $ { l }_{ 1 } = 160 cm $ und $ { l }_{ 2 } = 20 cm $ und $ { F }_{ 1 } = 250 N $ gesucht ist die Größe von $ { F }_{ 2 } $ in Newton.
Die konkreten Werte in das Hebelgesetz eingetragen, führt zu dieser Formel:
$ 250 N \times 160 cm = x \times 20 cm $
Diese Gleichung kann einfach nach $ x $ aufgelöst werden, $ x $ steht in diesem Fall für $ { F }_{ 2 } $:
$ x = \frac { 250 N \times 160 cm }{ 20 cm } $ → $ x = { F }_{ 2 } = 2.000 N $
Die Kraft am langen Hebelarm wird mit einer Federwaage gemessen. Bei einer Federwaage wird eine Schraubenfeder proportional zu der wirkenden Kraft gedehnt (Hookesches Gesetz). Eine Federwaage ist nichts anderes als ein Kraftmesser, der Kilogramm anzeigt.

Kilogramm (kg) kann einfach in Newton (N) umgerechnet werden. Ein Massestück mit einer Masse von $ 1 kg $ wird mit einer (Gewichts-)Kraft von $ 9,81 N $ von der Erde angezogen. Es rechnet sich einfacher, wenn wir für $ 1 kg $ eine Gewichtskraft von $ 10 N $ verwenden.
Wenn die Waage also $ 23 kg $ anzeigt, dann wirkt eine Kraft von $ 230 N $ auf die Federwaage.
Vielleicht hast du es bemerkt: Der „Zeiger“ der Federwaage hat einen Magneten verschoben. Die Position des Magneten zeigt die Kraft an, bei der die Brücke nachgegeben hat.
$ { F }_{ 2 } = \frac { { F }_{ 1 } \times { l }_{ 1 } }{ { l }_{ 2 }} $ → $ { F }_{ 2 } = \frac { 230 N \times 160 cm }{ 20 cm } $ → $ { F }_{ 2 } = 1.840 N $
Das entspricht einer Belastung von $ 184 kg $. Ganz schön stabil die kleine Brücke!
Hält deine Brücke dem „Brücken-Knacker“ stand? Nimm an der Brücken-Challenge teil und finde es heraus.
… wird hier veröffentlicht.
1. Brücke
Die Brücke von P. H. aus der 9f im Belastungstest.
Die Brücke hat standgehalten, die Durchbiegung war minimal. Die Kraft, welche am langen Hebelarm wirkte, betrug etwa 260 N.
$ { F }_{ 2 } = \frac { { F }_{ 1 } \times { l }_{ 1 } }{ { l }_{ 2 }} $ → $ { F }_{ 2 } = \frac { 260 N \times 160 cm }{ 20 cm } $ → $ { F }_{ 2 } = 2.080 N $
